Parameter Vs. Statistic: What Are The Differences?

Let’s talk numbers! Statistics and parameters are quite similar, as they both describe groups, such as “5% of students like to talk about data analysis”.

However, many have trouble understanding these two terms and telling the difference between parameter and statistic. Let’s take a closer look at both measures and see what exactly they refer to and what distinguishes them.

 

Parameter

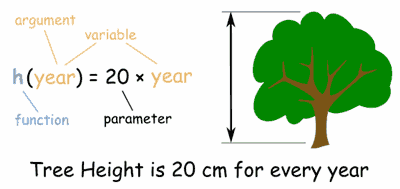
A parameter is a measure or characteristic (such as mean, median or average and mode) describing a whole population based on all the elements within that population. In statistics, population refers to the aggregate of all units taken under study which share similar characteristics.

For instance, all the students in a classroom can be considered a population, just as well as all women on earth, or all elements in the periodic table, or even a shopping trolley.

For instance, if you ask all students in a classroom what kind of ice cream they like and half of them say chocolate, we’re talking a parameter here: 50% of the whole class (our population in this case) likes chocolate ice cream.

On the other hand, it would be impossible to count how many women in the whole world like chocolate ice cream, as you can’t ask all of them about their preferences.

In this case, you would usually survey just a portion of them (a representative sample) and extrapolate the answer to the whole population. And this takes us to our next measure:

 

Statistic

A statistic is a measure or characteristic that states something about a sample (just a portion of the population under study). In inference analyses, a statistic acts as an estimator for parameters – using data about a sample, you can estimate the characteristics of a whole population. There are two types of statistics descriptive and inferential.

Therefore, if you see something like  “20% of dog owners worldwide pick up after their pets when out on walks”, you’ll know this is a statistic, as no one could have surveyed absolutely all dog owners in the world – they must have used a sample to estimate a percentage.

 

The Differences between Parameter and Statistic

Do you have a better grasp of the difference between statistics and parameters now? Check out the parameter vs statistic table below for a side-by-side comparison:

Parameter	Statistic
A parameter describes a whole population.	A statistic describes a sample but can be used to estimate the characteristics of whole populations.
A parameter is a fixed, unknown value.	A statistic is a known variable that depends on the sample.
In most cases, a parameter is not directly observable and calculable(unless we’re talking about very small populations which can easily be surveyed or observed in their entirety).	A statistic is easily observable and directly calculable.
In case of parameters, the Greek letter “mu” represents the population mean.	In case of statistics, the “x-bar” symbol represents the sample mean, and most other notations differ too.

Did our post manage to help you see the exact differences between parameter and statistic? Subscribe to our newsletter to learn more answers that can aid you in your studies or get fascinating topics about the world around you straight to your inbox!