Difference Between Mean, Median, and Average

One of the first things you learn in statistics is mean, median, mode, and average. It’s one of those things that doesn’t quite leave us after graduating from high school.

You need to calculate these values in any running business as they are a standard form of data analysis.

Because this is an important method of measure, you need to be quite clear on which one to choose when it comes to mean vs median vs average. These are different things used to measure different aspects of given information.

Whether you want to learn math yourself or want to help out your kid, here’s everything you need to know about mean, median, and average!

What Is Mean?

Mean is the average of a sample. In statistics and real life, this is a measure that is used most often.

Uses of Mean

One of the most important uses that the calculation of the arithmetic mean value is to serve as a yardstick for a set of information. You get an idea about the numbers on average. For example, you could use mean to find out the average work hours of a group of employees. You could then use this value as a standard measure.

For example, the calculated mean in a company for average working hours is 8 hours. An employee that has worked for 6 hours can be labeled as not trained enough. And an employee who has worked over 8 hours, which is the average working hours, has done more training than required.

Similarly, you could use this sort of data to compare and contrast information between a larger group of working people and a small group, a group of women and a group of men, etc.

What this does is that it provides a value that you can set as a standard to compare data.

You could also use mean to find out data about wage and budget increases and decreases in a company. For example, if you know the mean wage, you can figure out how much it would cost you to increase the wage by 4% for all workers. The calculation is much simple and quicker this way.

How to Calculate Mean

Calculating the mean of a given set of data is pretty easy.

For example, the set of numbers are:

73, 73, 76, 77, 81, 100

To find out the mean, you need to divide the total of observations by the total number of observations in a given set.

Step 1: Find the Sum

So, for this one, the total of observation in the set is 73+73+77+76+81+100=480

Step 2: Divide Sum by Number of Observations

The number of observations is 6.

To get the mean value, you divide 480/6. 80 is your mean value.

Major Differences Between Inner Join and Outer Join

What Is Median?

Median is also a kind of tool to present a measure of data in a group of numbers. In simple words, the median is used to find out the value in the middle of a set of data.

Uses of Median

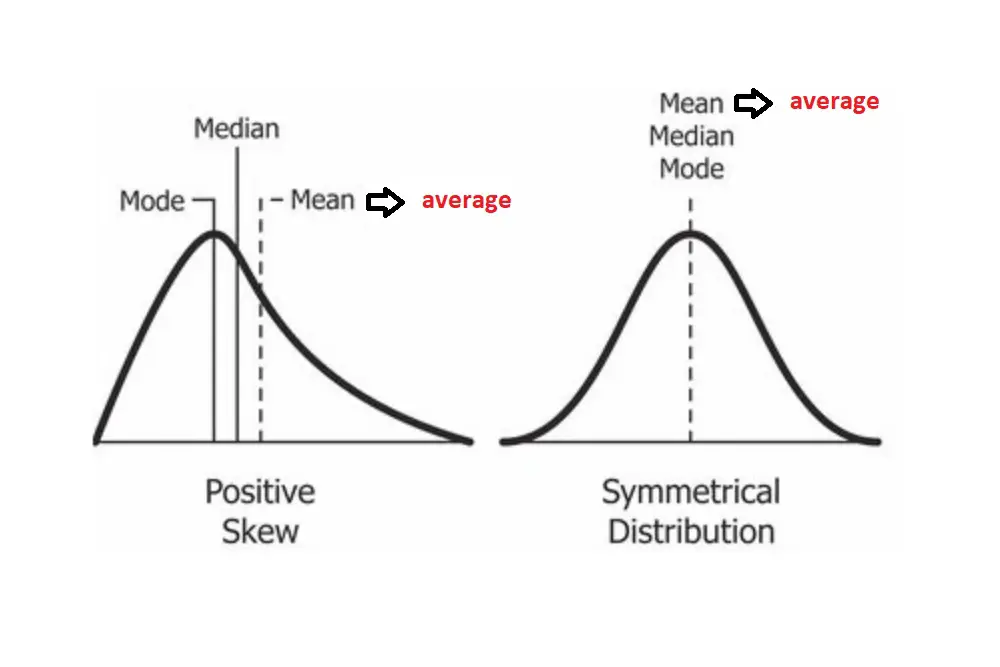
An advantage of using median instead of mean or average is that the result does not skew. When calculating an average value, just one single large or small number in the given data can drastically alter the result; this might not always be a practical approach.

For example, when calculating the height of a group of athletes. If out of six players, one player is extremely short or extremely tall, the average height for the group will change to an untrue result; this is where calculating the median is beneficial.

Median is used as a method of data presentation when:

You need to find out the midpoint of the distribution.
When there is an anomaly or extreme value.
To find if a value settles in the upper half or lower half of a distribution.

How to Calculate Median

For example, you have been given a set of values:

1,9,8,7,3,6,3

Step 1: Organize in Ascending Order

The first step is to organize them in ascending order.

So now the numbers would be:

1,3,3,6,7,8,9

Step 2: Find the Number in the Middle

Here the number 6 is in the middle and is, therefore, the median.

But what if the numbers of values were even?

For example,

1,9,8,7,3,6,3,2

Step 1: Organize in Ascending Order

Firstly, you would arrange the numbers in ascending order

So, you have:

1,2,3,3,6,7,8,9

Step 2: Find the Numbers in the Middle

Now in the middle, you have: 3 and 6

Step 3: Divide the Sum of the Middle Values by 2

To calculate the median, you add the numbers in the middle and divide them by 2.

So now the median is 9/2, so 4.5

What Is Average?

This is a confusing part. You will realize, when calculating, that average and mean are the same. Well, they are. There is little to no difference between them.

The only notable difference you will find between them is in the textbook definition.

An average is when you divide the sum of all the given values by the total number of values. And mean is when you divide the total sum of observations by the number of observations in a given sample of data set.

Give the definitions a couple of reads, it’s pretty much the same thing, right?

While the method of calculation also remains the same, you might find a little bit of a difference in the use of the methods.

We typically use the mean to get a central tendency measurement; this is when you are provided with group data such as in statistics. We use the average as a more general approach. One could use average to calculate the mean of the numbers.

You will see the use of the term ‘average’ in newspapers and articles. The value is used when there is large-scale data, unlike group data.

Some of Our Articles You May Want to Read:

Mean vs Median vs Average: The Main Differences

Here is a chart to show you some more key differences between mean, median, and average.

Parameter	Mean	Median	Average
Value It Gives	Only Mean	Only Median	Average, median, and mode
Definition	Mean is when you divide the total sum of observations by the number of observations in a given sample of the data set	Median is used to find out the value in the middle of a set of data	An average is when you divide the sum of all the given values by the total number of values
Varieties	Can be of various types; arithmetic, weighted or geometric	Comes in multiple varieties. For example, cumulative frequency	Comes in means of mean, median, and mode

Key Takeaways

The difference between mean and average is that mean uses data in a given set, and average is more general.
Mean, or average, is used as a standard measurement for an observation.
Median is the middle value in a group of observations.
Mode is used when there is a number with a large-scale difference in the set.

Final Words

Now that you know which one to go for in the battle of mean vs median vs average, you should be able to present your data more easily.

When used correctly and in the right place, these methods can be great for any kind of quantitative and analytical measure.

Difference Between Mean, Median, and Average